Research
I use mathematical and computational methods to understand dynamics and function of neural systems. Much of my research is particularly focus on specialized neurons and neural circuits in the auditory system. The auditory system is tasked with constructing perceptually-rich auditory scenes from time-varying inputs. The study of this system is, therefore, fertile ground for dynamical systems, differential equations, stochastic processes, and related mathematics that describe the evolution of systems over time.
By taking this system-specific approach, I have been able to participate in meaningful and productive collaborations with specialists in hearing science, auditory neuroscience, and biomedical engineering, and audiology. Major contributions include developing models of neural response to cochlear implants, biophysically-based modeling and interpretation of in vivo extracellular voltages in the auditory brainstem (the so-called auditory neurophonic), analysis of structural specializations of coincidence detector neurons in the auditory brainstem, and data analysis of multi-neuron recordings in auditory cortex. Other, more general, research contributions include development and validation of simulation methods for stochastic differential equations models of ion channel noise, and gain control effects of A-type potassium channels.
Further details are available in my publications, listed here.
I work with Swarthmore students on summer research projects; see more information and examples of past projects HERE. I collaborate enthusiastically with mathematicians, auditory neuroscientists, hearing scientists, and others with related interests. I
I am grateful for funding support from predoctoral and postdoctoral fellowships from NIH Institute on Deafness and Other Communication Disorders (F31 DC010306 and F32 DC012978) and NSF Division of Mathematical Science (RUI 1951436).
I gave a short overview of my research at the 2017 Swarthmore College Faculty Showcase (Nov 10, 2017), and include it below:
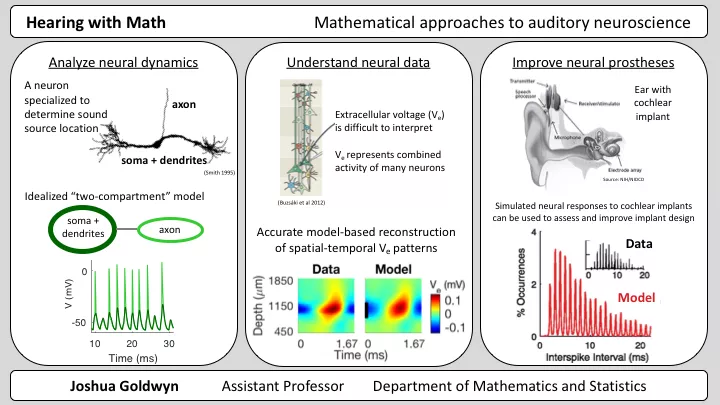
Three ways in which I apply mathematics to understand the auditory system
Analyze neural dynamics
I develop mathematical models to describe the dynamics of neurons in the auditory pathway. The neuron pictured in the first column is in a region of the brain called the medial superior olive (or MSO). What’s remarkable about these neurons, is that they are able to compare the timing of sounds arriving at our two ears with microsecond-scale temporal precision. This exquisite timing calculation allows us to sense the spatial locations from which sounds originate.
I am currently working to understand how the structure of these cells affects their dynamics and function. Specifically, I am determining how the coupling between the axon and the cell affects the temporal precision of MSO neurons. To do this, I construct an idealized mathematical model of the neuron. I imagine that the cell can be lumped, roughly, into two regions: the axon (output) region and the remaining (input) regions. I then systematically explore the behavior of my mathematical neuron model as I change the connection between these regions.
This approach of formulating minimal, or idealized models, is a common strategy across my work. I use it to uncover essential properties of complex systems.
Understand neural data
I also develop mathematical models and methods to understand neural data recorded by experimental collaborators. One type of data that is relatively easy to obtain but difficult to understand is extracellular voltage. Extracellular voltages are recorded in the space between neurons. These signals represent a complicated mixture of the activity of many neurons.
I recently worked with expert collaborators who recorded extracellular voltage signals in auditory regions of the brain. I developed a model that successfully reproduced the spatial-temporal patterns of extracellular voltages recorded by my collaborators, as shown in the middle column. Using this model, we gained new understanding of these complicated neural signals.
Improve neural prostheses
Unfortunately, the auditory system does not always work flawlessly. For some individuals with profound hearing loss, surgically implanted devices called cochlear implants can restore a sense of hearing by electrically activating neurons in the inner ear. I have developed models to accurately simulate the responses of auditory neurons to cochlear implants, as shown here. I can then use this model to evaluate cochlear implant designs, by quantifying how effectively sound information is provided to users of these devices.
This project is especially gratifying because it represents an opportunity to use mathematics to improve the quality of life of individuals with hearing impairment.