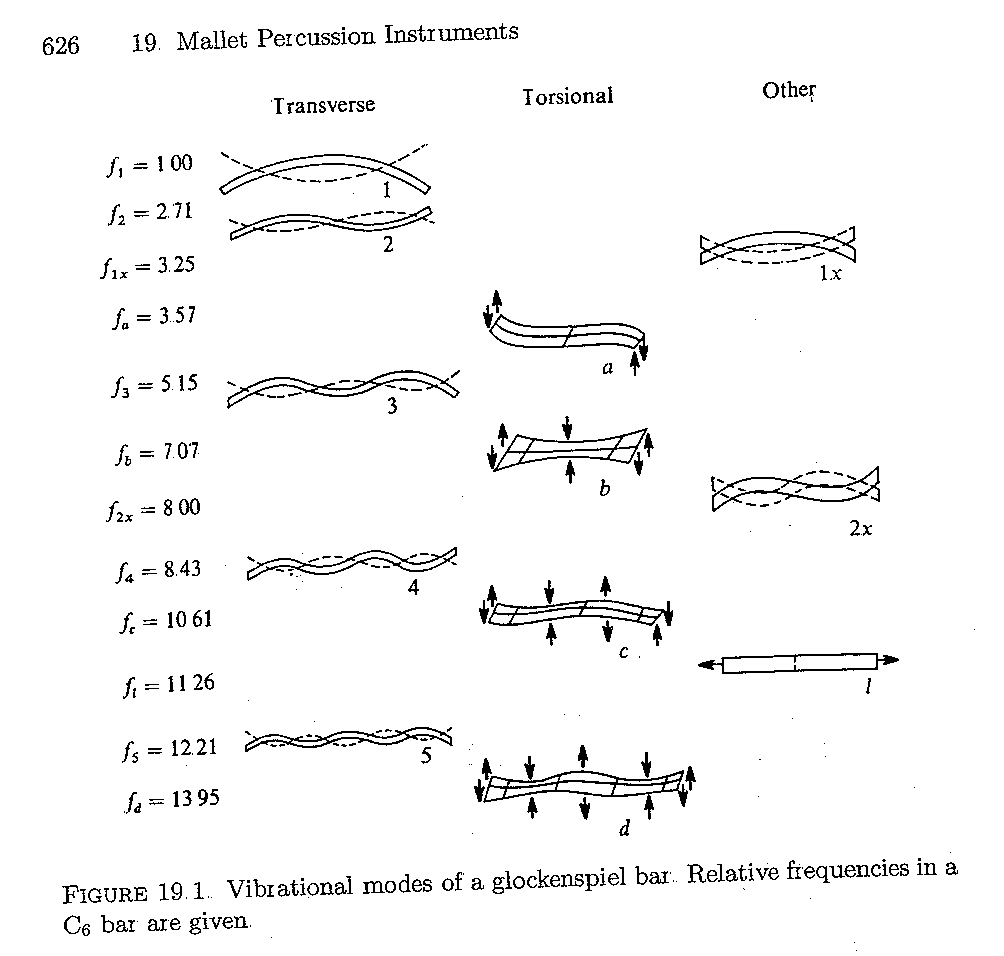
Welcome to the third lab in E5, where you will begin to fabricate parts for your group's instrument in the Machine Shop in the basement of Papazian (next to Hicks).
A reminder of the lab groups :
| Lab A | Lab B | Lab C |
Group A1: Hurdy Gurdy
|
Group B1: Hurdy Gurdy
|
Group C1: Hurdy Gurdy
|
Group A2: Glockenspiel
|
Group B2: Glockenspiel
|
Group C2: Glockenspiel
|
Group A3: Pennywhistle
| Group B3: Pennywhistle
|
Group C3: Pennywhistle
|
Group A4: Pennywhistle
|
At the end of class on Tuesday I began to talk about the basic physics of how our musical instruments work. Very briefly, all musical instruments produce periodic vibrations which register as "pitch" to human listeners. The more periodic(repetitious) the waveform, the stronger the sense of pitch. If the frequency components that make up the sound are related by integer multiples (harmonics), then the waveform will be very periodic. If the frequency components are inharmonic, then a "clang" component to the sound will be heard, and the sound will have less of a sense of what note is being produced (think of snare drums vs. tom-tom drums vs. kettledrums).
For strings fixed and tubes open at both ends, the boundary conditions on both ends are identical and the one-dimensional wave equation has a solution consisting of multiples of half-wavelengths. Each mode of vibration occurs at a frequency given by f = nv/2L, where n is an integer n = 1, 2, 3, 4, ... corresponding to the harmonic number (where the lowest note n=1 is the fundamental frequency). L is the length of the string or air column and v is the wave speed (v = 343 m/s for air at 25°C, or v = sqrt(T/rho) for a string of mass-per-unit-length rho and tension T). The fundamental frequency is what is usually perceived as the pitch of the instrument, while the relative amplitudes of the harmonic modes affect the timbre (pronounced "TAM-ber") or tone color of the instrument.
As I mentioned on Tuesday, the location of the point at which the string or air column is excited or stopped affects which of the possible modes (and their corresponding frequency components) are allowed to remain in the vibration recipe. Thus a pressure node (negligible fluctuation in acoustic pressure) occurs wherever a hole is placed in air-filled tube, and a displacement node occurs wherever a player's finger rests lightly on a string. Only modes with nodes at these points are allowed to exist; the lowest-frequency one (usually) determines the perceived pitch. Conversely, the pluck or bow-contact point of a string eliminates from the vibration recipe all those modes with nodes there. For instance, plucking or bowing a string 1/5 of the way along its length eliminates the 5th harmonic (because it has a node there), as well as the 10th, 15th, 20th, 25th, etc. harmonic (because they too have nodes there).
This situation for glockenspiel bars is a bit different, because the bar is a 3-D object and supports longitudinal, flexural, and torsional modes of vibration simultaneously. Here is a page from Fletcher and Rossing's book "The Physics of Musical Instruments:"
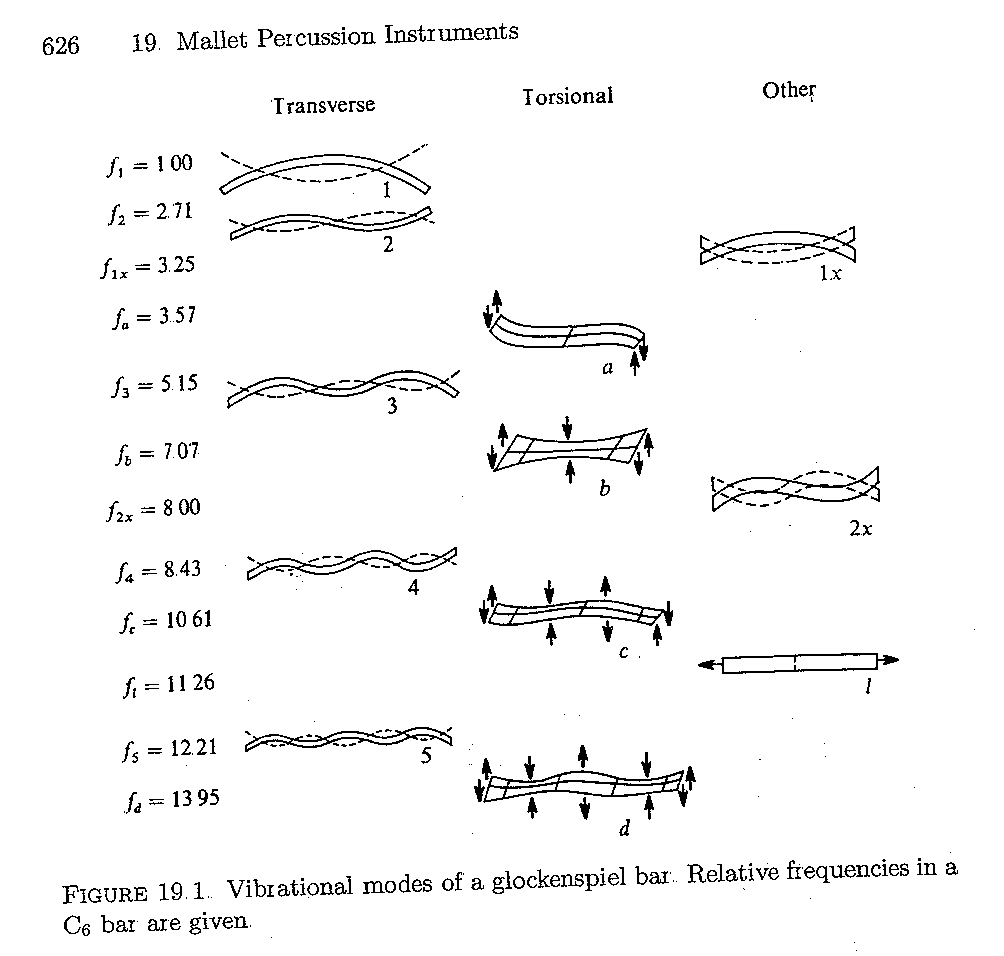
Moreover, as you can see from above, the modes are no longer harmonically related. It is beyond the scope of E5 to derive the 3-D wave equation and find the solution, but if you are interested, ask me. Here's the solution for transverse bending waves (y is the vertical displacement of the centerline from equilibrium):
y = cos(ωt + φ)[A cosh(ωx/ν) + B sinh(ωx/ν) + C cos(ωx/ν) + D sin(ωx/ν)]
where ω = 2πf is the angular frequency, x is the distance along the bar in the long direction, and ν = sqrt(ωcκ), where c is the wave speed in the bar and κ is the "radius of gyration" equal to the bar thickness divided by square root of 12 (for bars of rectangular cross-section). For steel bars, c = 5050 m/s and for aluminum c = 5150 m/s. The coefficients A, B, C, and D are calculated once the boundary conditions are specified. For our bar, both ends will be free to move and so A-C = 0 and B-D = 0 at x = 0 and x=L.
The only frequencies that meet these conditions are those that satisfy the following transcendental equation:
tan(ωL/2ν) = tanh(ωL/2ν), where L is the length of the bar. These turn out to be given by
f = (πcκ/8L2) (3.011, 22, 52, 72, 92,...)
which are approximately the measured relative frequencies shown in the figure above.
As mentioned in class, we will be using a microphone and spectrum analyzer in lab this week to measure these frequencies, and see what happens when we undercut the bars in the center so as to reduce the bending stiffness in the center of the bar, while leaving the ends to flex. Those working on the glockenspiel will have to adopt this semi-empirical approach to tuning the bars.
More later for everyone on the relationships between different notes in the equal-tempered scale. We want your instruments to be in tune!
|
Comments
or Questions? |
|
 |