Arrays: Vectors and Matrices

Vectors

Vectors are an efficient notational method for representing lists of numbers. They are equivalent to the arrays in the programming language "C" that we learned about last week.

A typical vector might represent the high temperature every day for a week. Such a vector would have seven elements and could be written as a row vector (a single row),

or as a column vector (a single column),

Note, that I will use bold letters when referring to the entire vector (or matrix). In both cases above, the HighTemp vector has seven elements, representing Sunday through Saturday. To access the individual elements in the array we use an index. For example, the temperature Sunday would be accessed as HighTemp(1), and is equal to 25. Likewise HighTemp(4)=38 is Wednesday's high temperature.

Matrices

A matrix (singular of matrices) is for our purposes a series of numbers listed in two dimensions. As an example, consider high temperatures collected over a 28 day period (4 weeks). We could write the matrix as a single list 28 elements long, or as a collection of numbers (a matrix) that has 4 rows and 7 columns.

Now we need two indices to represent the numbers, one for the row, and one for the column. For example the high temperature on the 3^rd day of the 2^nd week is HighTemp(2,3) and is equal to 45. Note that the index for the column comes first.

We could also write the matrix with rows and columns interchanged. This is referred to as taking the "transpose" of the matrix.

Note that a vector is the special case of a matrix, where there is only one row or column. Also note that the two vectors given are transposes of each other.

In general a matrix consisting of m×n elements can be arranged in m rows and n columns, yielding an mxn (read m by n) matrix, which we'll call A.

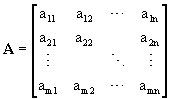
The symbol a_ij represents the number in the i^th row and the j^th column.

Matrix operations

For the ensuing discussion assume we have three matrices

Equality

Two matrices are equal if they are the same size, and corresponding elements are equal. For example, A=B, but A¹C.

Addition

Two matrices can be added if they are the same size. Their sum is given by a third matrix whose elements are the sum of the corresponding elements being added.of the two arrays If D=A+C then

Note that A+B=B+A.

Multiplication by a scalar

A matrix can be multiplied by a scalar (a scalar is a single number) by multiplying each element of the array by that number. For example:

Multiplication of two vectors

A row vector can be multiplied by a column vector, in that order, if and only if the have the same number of elements. If

then

For example:

Multiplication of two matrices

Two matrices, A and C can be multiplied together in the order AC if and only if the number of columns in A equals the number of rows in C. If D=AC, then d_ij is the element obtained by multiplying the row vector represented by the i^th row of A by the column vector represented by the j^th column of C. For arrays A and C with n columns and rows, respectively, we get:

For example, if D=AC, using the matrices given previously

Note that in general AC¹CA. In this case

ÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈÇÈ

Important matrices

Identity Matrix

There is a special matrix called the identity matrix. This is a square matrix has one's along the main diagonal, and 0's elsewhere. Shown are 2x2 and 4x4 identity matrices.